文章标题：Machine Learning K-Means Clustering of Interpolative Separable Density Fitting Algorithm for Accurate and Efficient Cubic-Scaling Exact Exchange Plus Random Phase Approximation within Plane Waves

通讯作者：张振林，银栖麟，胡伟*，杨金龙*

作为当今材料计算方法中的主流方法之一，密度泛函理论(DFT)因其准确性和广泛的通用性而闻名。在DFT理论中，材料的电子结构和性质是电子密度的泛函，其中对计算结果准确性起决定性作用的是交换关联泛函，对交换关联泛函的探索被Perdew 在他的“雅各布天梯”（Jacob’s ladder） 中分为五类。

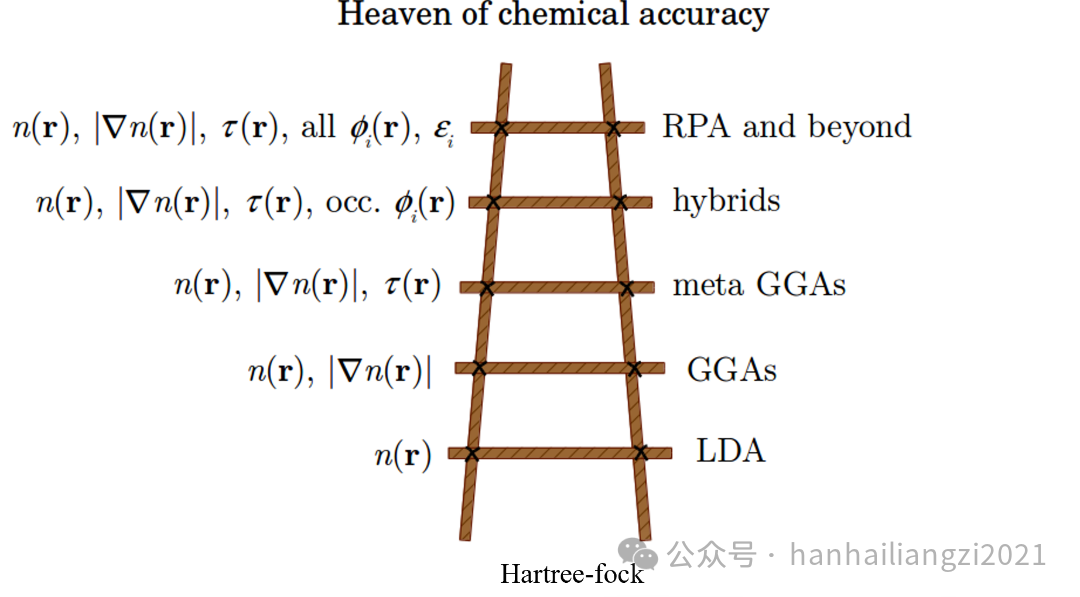
图1 雅各布天梯

其中的第五阶泛函，是目前最高等级的泛函，包括双杂化泛函(Double Hybrid functional)，精确交换+RPA关联能（EXX+RPA）等，EXX+RPA方法能够准确捕捉系统中的关联效应，更好的描述长程范德华作用，这对于理解材料性质（特别是弱相互作用的材料）至关重要。

然而，EXX+RPA的计算量与电子数目的四次方成正比，计算标度为O(N4)。在平面波基组下，EXX的计算标度为O(N4)或O(N3)，RPA的计算标度为O(N4)，而且具有很大的指前因子，这昂贵的计算代价使得EXX+RPA一直以来只用于小规模的电子结构计算。

尽管之前有一些三次标度的算法被提出，如使用柯西积分解耦与ISDF算法结合，但其巨大的指前因子仍然使得大规模计算难以实现，因此探索一种新的计算RPA关联能的算法势在必行。 

  
为了克服传统ISDF算法的限制，本文引入了一种增强的机器学习K-means方法。作者创新性地提出了一种经验权重函数“SSM+”，该权重函数可更精确地选择插值点，因此能够更准确地捕捉不同系统中的物理信息。这种机器学习方法计算插值点的标度为准二次，有效替代了基于平面波的EXX+RPA计算中昂贵的三次标度QRCP算法。该方法可以将RPA的计算标度从3.39降低到2.22，将EXX的总体计算标度从2.74降低到2.10。

作者使用基于MATLAB平台的第一性原理计算软件KSSOLV开发，可以使用MATLAB集成的GPU工具包来加速计算，实现了高达35倍的GPU加速。对于CPU计算时间，标准的四次标度方法需要22小时来计算Si128，使用K-means算法可将时间缩短到800秒，与标准四次标度算法相比，实现了高达100倍的加速。
通过这个改进的算法，作者对G2分子测试集的一些分子进行了测试，得出了与ABINIT高度一致的计算结果；作者成功计算了H2的解离曲线，给出了解离极限时曲线趋于零的正确趋势；最后，作者使用该方法正确预测了C18分子的平衡几何结构，与CCSD的计算结果一致。

（1）为了研究计算体系和算法参数对精度的影响，作者选取了四个对称性不同的分子，选用不同的K-means经验权重函数：SSM、PSM、SSM+(本文)，逐渐增大秩参数观察RPA关联能的收敛趋势以及绝对平均误差(MAE)变化情况。如下图所示，结果表明，随着秩参数（辅助基组数量Naux与秩参数成正比）增大，RPA关联能逐渐趋近于参考值Eref。SSM因为不能准确捕捉占据态信息，表现最差，几乎不能收敛；PSM可能会出现过拟合的情况，在某一秩参数之上误差陡然增大；而SSM+赋予占据态和未占据态相等的权重，随着秩参数的增大其计算精度表现出稳定和连续的收敛性质。

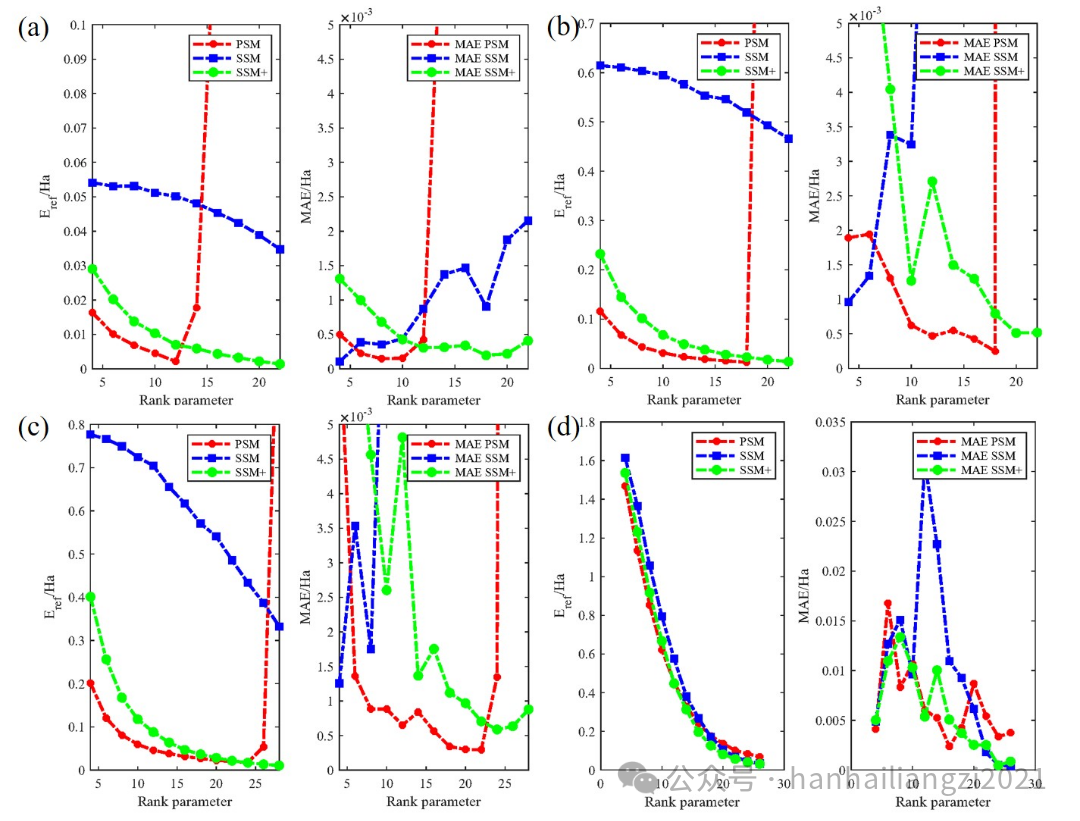
图2 四种对称性不同体系的权重函数测试 (a) H2 (b) CO (c) CH3OH (d) Si8

（2）为了测试本文算法的性能表现，作者使用三种不同的算法：标准算法、QRCP计算插值点、K-means计算插值点对不同大小的单Г点fcc硅体系进行了单线程测试（Si8-Si128）。对计算时间的标度拟合表明，对于EXX，ISDF(QRCP)计算标度与标准算法持平，但指前因子大于标准算法，ISDF(K-means)标度为2.10，小于标准算法2.74，但指前因子大于标准算法，其优势在大体系时才会体现出来。对于RPA计算， ISDF(QRCP)和ISDF(K-means)的拟合标度分别为2.56和2.22，而且指前因子比标准算法低。ISDF(K-means)大大降低了RPA的计算量，对于Si128这种大体系的RPA关联能计算，标准算法计算时间为79329s，ISDF(QRCP)计算时间为4156s，而ISDF(K-means)计算时间为800s，比标准算法快了近100倍。

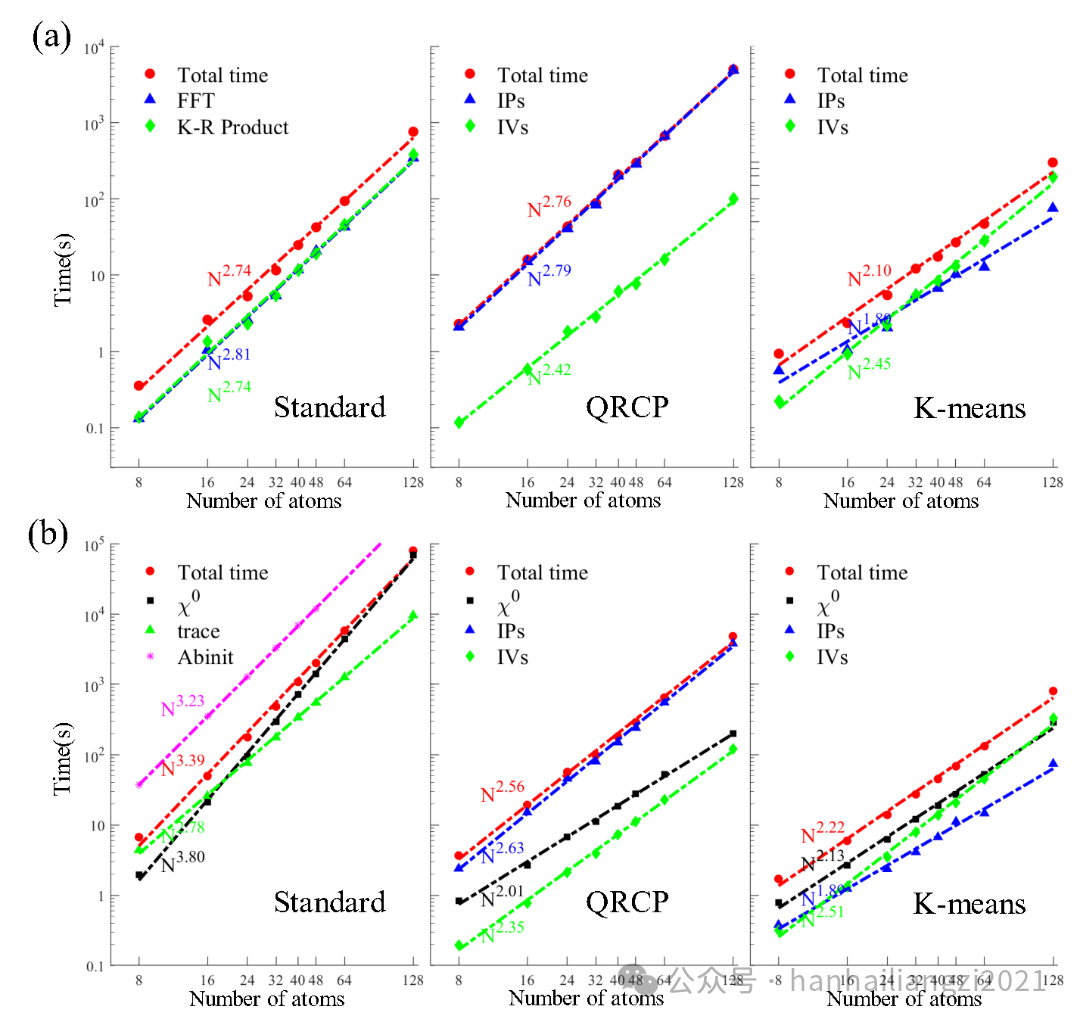
图3  EXX与RPA单线程计算时间随原子数目增大的变化 (a) EXX (b) RPA

（3）作者横向对比了ABINIT和Quantum Espresso的RPA计算功能。ABINIT目前只有标准算法（四次标度），Quantum Espresso使用cholesky分解来计算ISDF的插值点（三次标度）。计算体系仍然是fcc体相硅。结果表明，由于使用了K-means算法，KSSOLV的计算速度相比以上两款软件有了显著的提升。

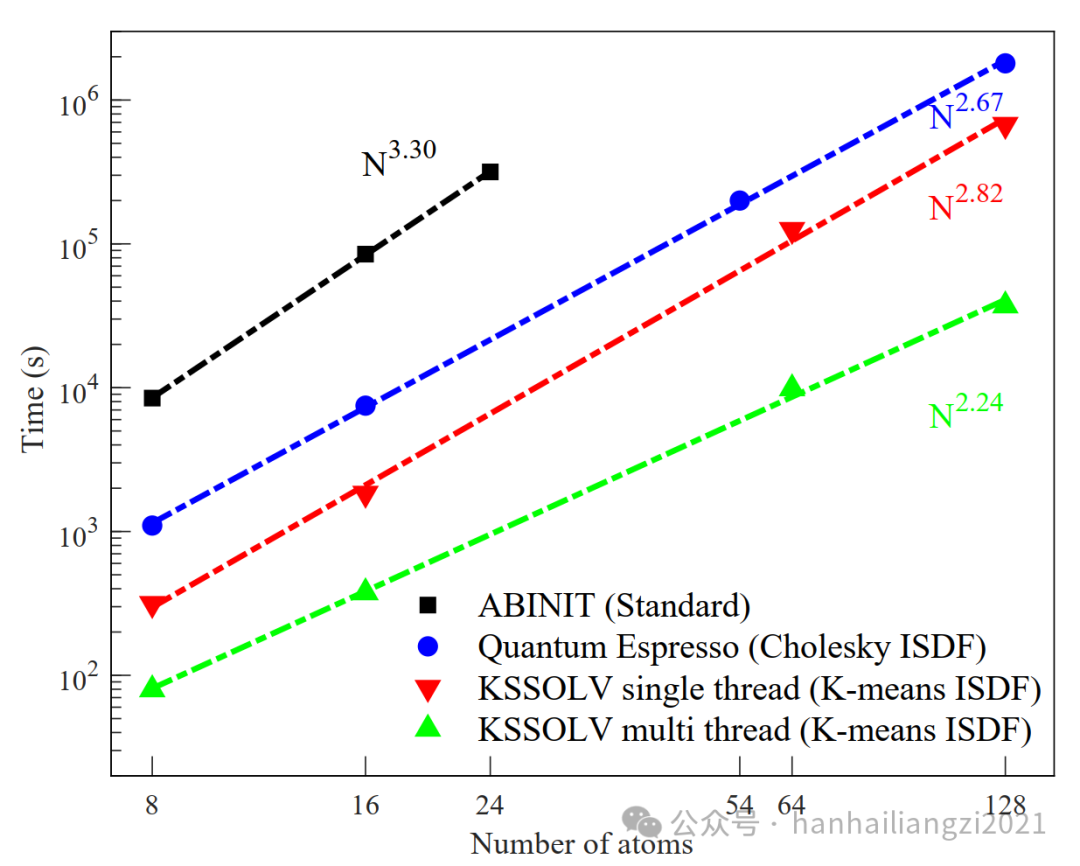
图4 不同软件的RPA计算时间对比 ABINIT、Quantum Espresso、KSSOLV

（4）作者测试了MATLAB中集成的GPU加速功能对算法的加速表现。如下图所示，GPU对于三种算法都有着不同程度的加速效果。其中QRCP加速效果最明显，对于Si48的RPA计算能加速18倍，对于K-means的加速比则能达到5倍。

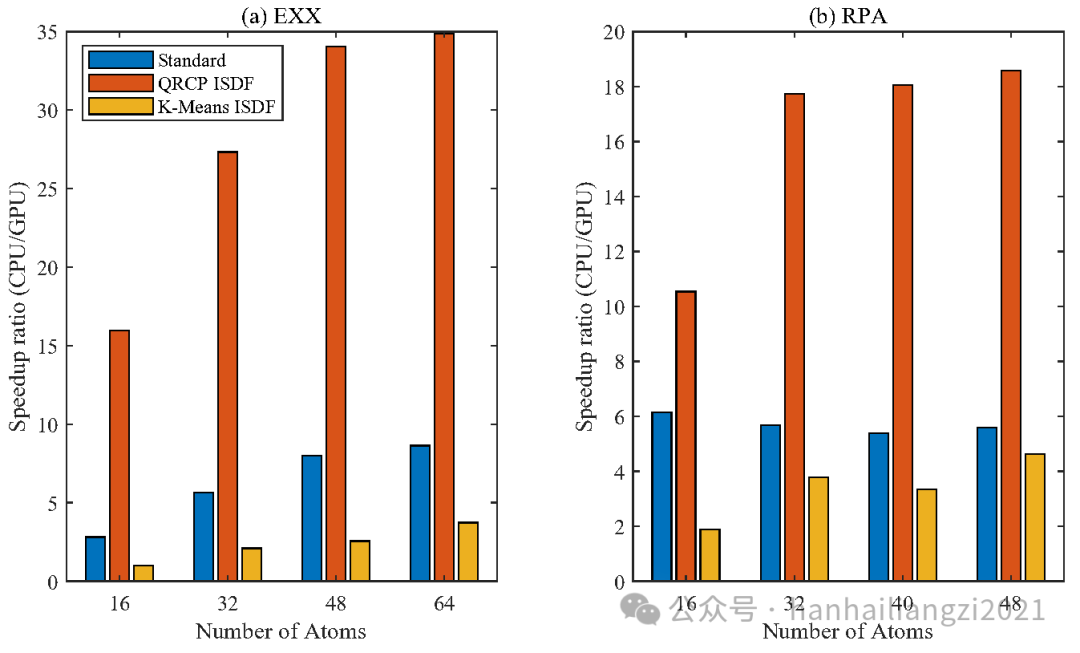
图5  GPU加速比 (a) EXX (b) RPA

（1）作者基于KSSOLV 中实现的EXX+RPA功能计算了H2的解离曲线。如下图所示，GGA-PBE计算的原子化能通常会在解离极限处高估2eV，而使用EXX+RPA框架能够准确描述原子化能在解离极限处趋于零的趋势。

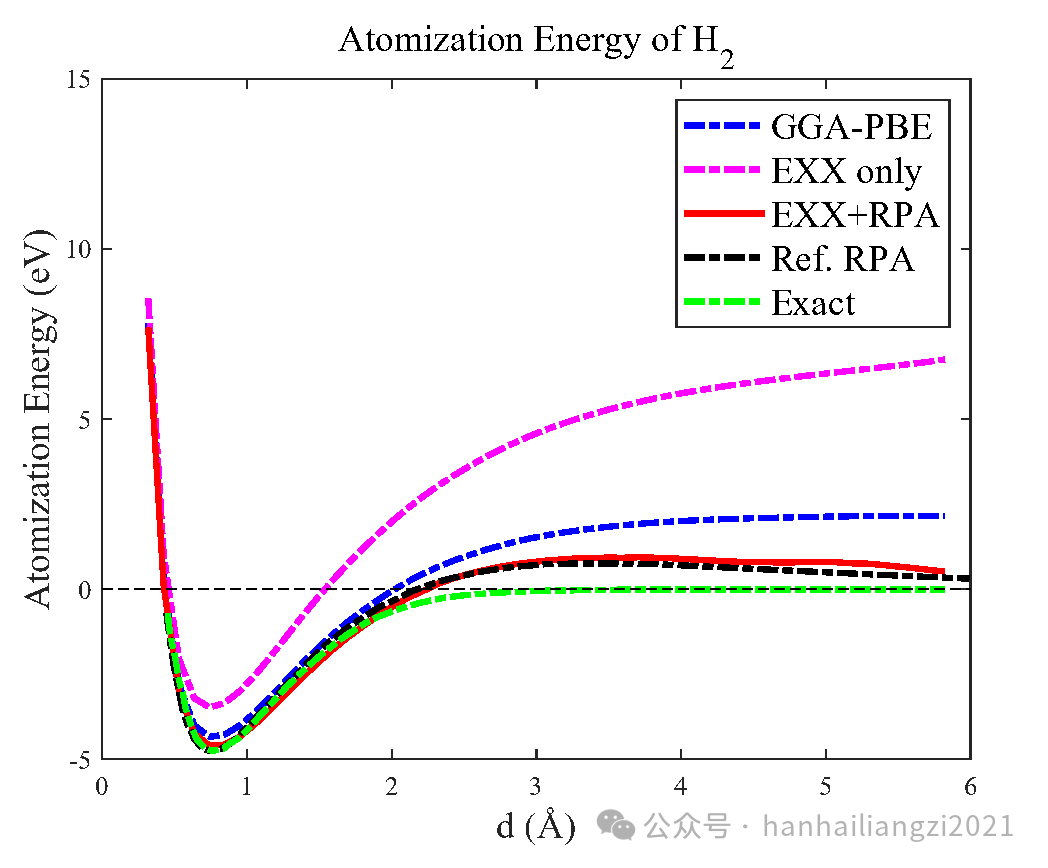
图6  H2的解离曲线

（2）作者基于KSSOLV的三次标度的EXX+RPA功能计算了C18的平衡构型。C18有两种可能的结构，一种是所有键全同，如图7上图的θ1=20°，一种是键长交替变化，即θ2≠20°。一般的DFT和微扰理论(MP2)预测出的是键全同的结构，而实验以及CCSD计算则表明真实结构是键长交替变化的。

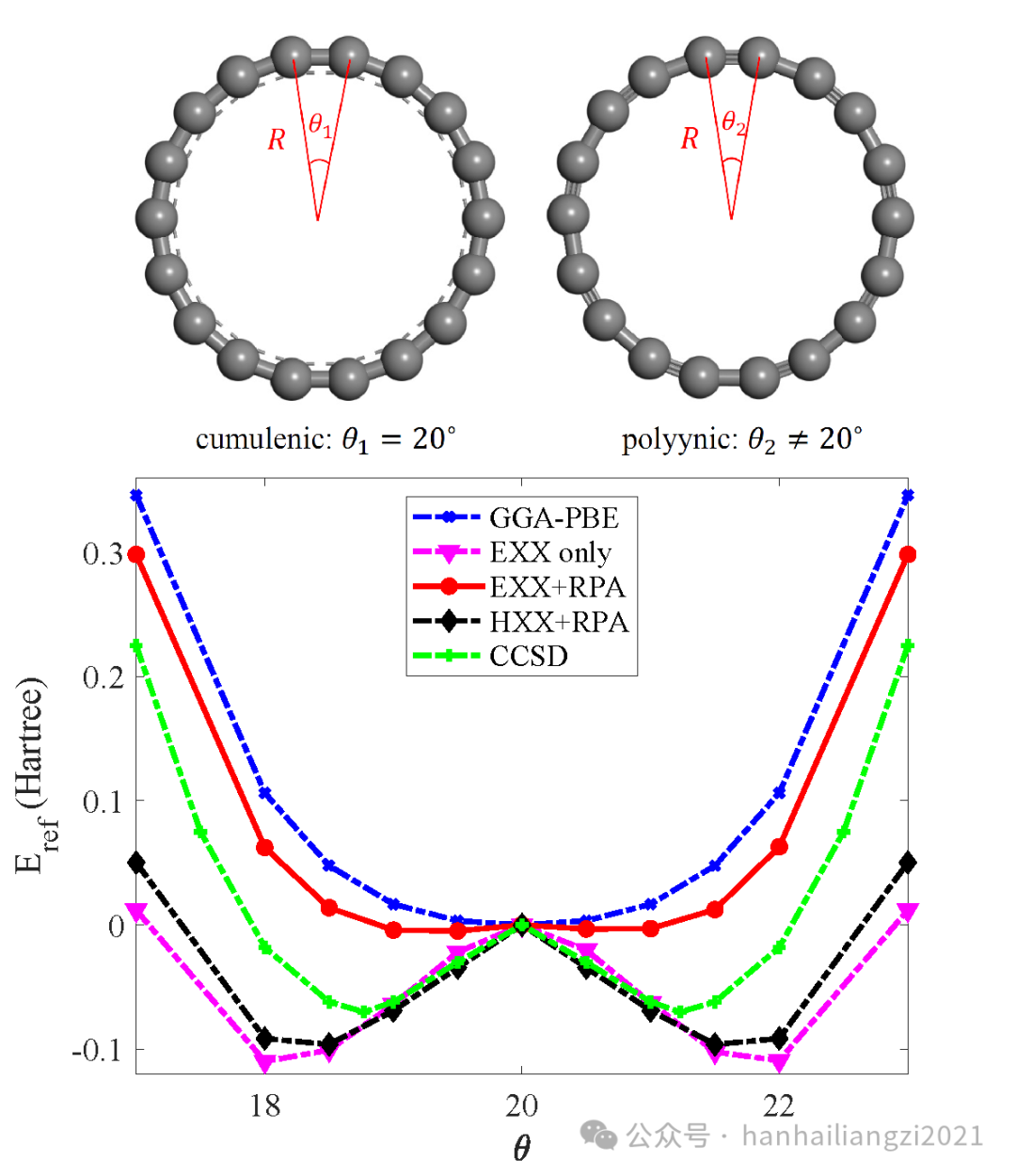
图7 （上图）C18分子结构示意图 （下图）GGA-PBE, EXX+RPA, HXX+RPA, EXX only, 

和 CCSD计算出的C18分子势能曲线对比

通过改变θ角（θ取值范围[0°,40°]），可以将计算出的总能量对θ=20°的总能量相对值Eref画出一条曲线，若Eref在θ=20°有极小值，则对应于键全同的结构；若Eref的极小值不在θ=20°，则对应于键长交替变化结构。计算结果表明，GGA-PBE预测的结构为键全同，而EXX only（只考虑EXX，不计入RPA关联能）、EXX+RPA、HXX+RPA（用HSE轨道计算EXX，用PBE轨道计算RPA）预测结构都是键长交替变化的，与CCSD一致。注意到EXX+RPA曲线的低谷相较CCSD曲线不明显，作者将其归因于EXX+RPA缺乏单激发贡献，所以计算不准确。通过使用HSE轨道计算EXX则可得到与CCSD更为接近的结果，即图中黑色曲线 。