近日,SC24在美国亚特兰大召开,SC会议全称为“The International Conference for High Performance Computing, Networking, Storage, and Analysis”,是全球高性能计算、计算机系统结构领域最具影响力的盛会之一。自1988年首次举办以来,SC会议已成为一个汇聚世界顶尖科学家、工程师、研究人员和企业领导者的平台,共同探讨和展示最新的科技成果和创新应用。
SC24共收到449篇投稿论文,录用102篇,录用率仅为22.7%。PWDFT的大规模GW计算成果以“Enabling 13K-Atom Excited-State GW Calculations via Low-Rank Approximations and HPC on the New Sunway Supercomputer”为题入选SC24会议论文。
文章介绍
GW计算是凝聚态物理学和材料科学中常用的重要计算方法,主要用于精准描述材料的电子结构。与传统的密度泛函理论(DFT)相比,GW方法能够显著提高能带结构的预测精度,特别在半导体材料、光电器件和太阳能电池等领域,展现出巨大的应用潜力。
在GW计算中,通过计算自能来修正密度泛函理论(DFT)中的交换-关联势,从而提高电子结构的精度。GW计算的主要瓶颈在于自能的计算,其计算复杂度为O(N⁴),存储复杂度为O(N³)。此外,由于计算中的置前因子较大,介电矩阵的求逆也是一个重要的瓶颈,其计算复杂度为O(N³),存储复杂度为O(N²)。另一个挑战是极化率的计算,其计算复杂度为O(N⁴),存储复杂度为O(N³)。其中,N表示体系中的电子数。由于较高的计算和存储复杂度,随着体系规模的增大,计算成本和存储需求迅速增长,严重限制了大规模GW计算的应用。目前,最大的模拟体系由BerkeleyGW使用27648个V100 GPU模拟2742个原子,并因此获得了2020年ACM Gordon Bell Prize Finalist。然而,巨大的计算量和存储需求使得实现更大规模的计算面临极大的挑战。
表1 大规模GW计算研究进展及性能对比

在这项工作中,来自中国科学技术大学、复旦大学和崂山实验室的研究人员通过数值算法与高性能计算的协同设计,加速了GW计算。他们通过一系列低秩算法成功降低了主要计算瓶颈的计算复杂度和内存需求。同时,充分利用相关超算平台的特点,优化了数据传输过程,提高了数据移动与通信效率,从而最大限度地发挥了超算算力的优势。
数值算法
算法一:插值可分离密度拟合算法(ISDF)
在平面波基组中,许多算子可以表示为轨道对乘积的形式。由于轨道对乘积的行数和列数存在巨大差异,这表明其矩阵具有低秩性质。因此,可以利用低秩算法来降低计算和存储成本。插值可分离密度拟合算法是一种常用的低秩算法,已被广泛应用于其他电子结构计算方法,如杂化泛函计算和含时密度泛函理论。在插值可分离密度拟合算法中,轨道对乘积可以表示为一系列插值点与插值函数的组合。其指标可分离的特性使得可以交换求和符号,从而有效降低计算复杂度。
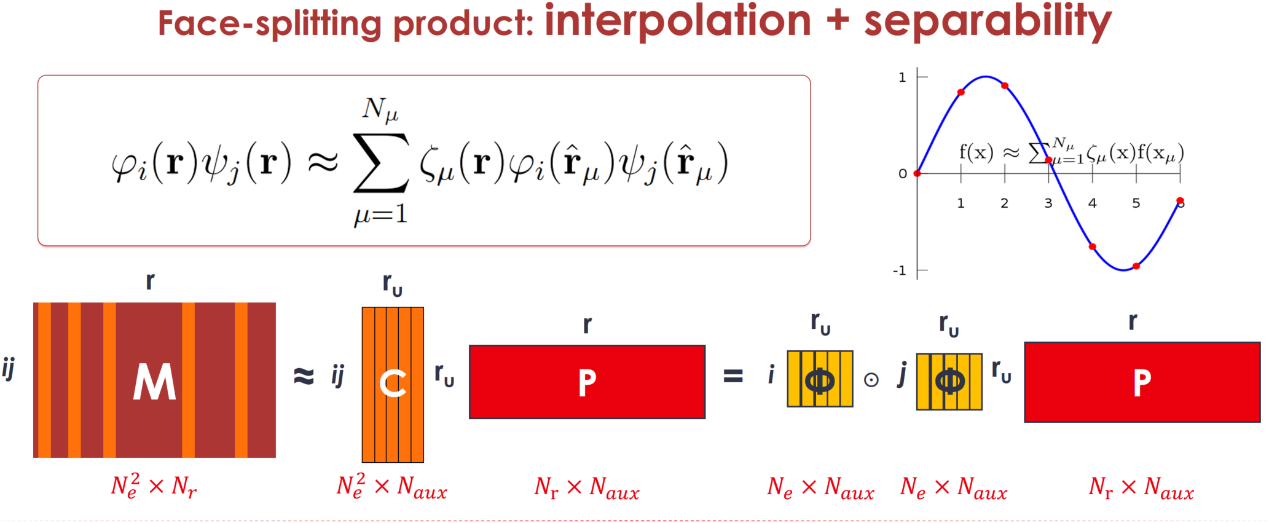
图1:插值可分离密度拟合算法原理。
算法二:机器学习K-means聚类算法
K-means算法是一种常用的机器学习聚类算法。在这项工作中,机器学习算法被用于寻找空间中最可分离的向量。使用轨道对乘积的平方和作为权重函数,度量标准选用平方欧几里得距离。由于K-means算法的计算和内存复杂度均为O(N2),同时具有很好的并行性,因此很适合大规模计算。
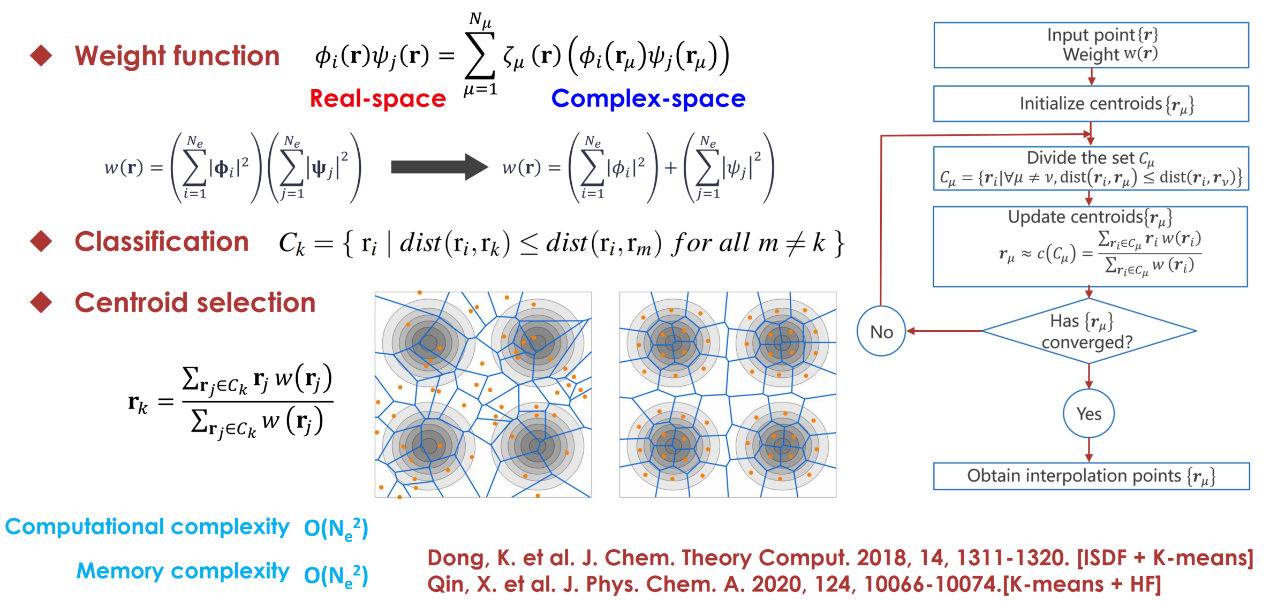
图2:K-means算法计算流程。
算法三:Sherman — Morrison — Woodbury 公式加速求逆
在标准GW计算,另一个计算瓶颈是介电矩阵的存储和求逆。Sherman — Morrison — Woodbury(SMW) 公式是线性代数中常用的矩阵求逆公式。我们通过将ISDF算法与SMW算法联用,将介电矩阵的逆表示成一系列小矩阵的乘积。同时将一个大矩阵的求逆转变为两个小矩阵的求逆,从而将计算和内存复杂度的置前因子降低,从而缓解计算和存储瓶颈。

图3:SMW公式计算过程。
算法四:柯西积分分离指标
在计算极化率时,由于能带指标的耦合关系产生了四次计算标度。在本项工作中,研究人员通过柯西积分的方法将指标分离开,积分曲线使用第一类椭圆积分,将计算复杂度从O(N⁴)降为O(N³),存储复杂度从O(N³)降到O(N²)。
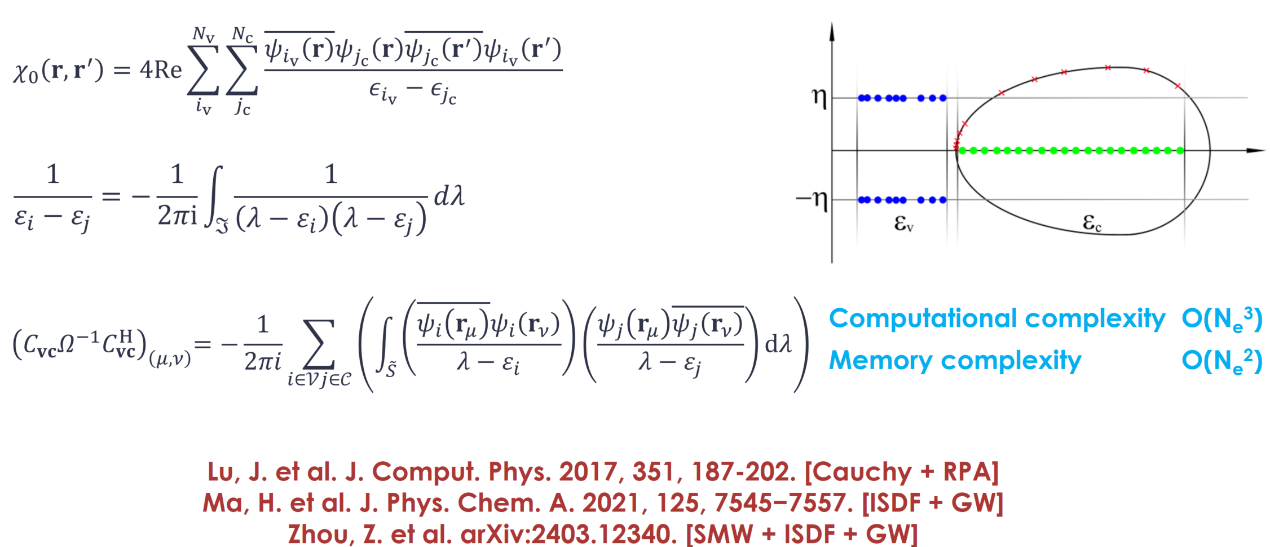
图4:柯西积分公式及积分曲线。
并行优化
所有的大规模模拟实验是在PWDFT软件中进行的,PWDFT是一款第一性原理计算软件包,支持HSE06,TDDFT和 GW计算,支持大规模电子结构计算。测试平台为最新的神威超算,每个节点含有六个核组。每个核组含有一个管理处理单元(MPE)和六十四个计算处理单元(CPE)。
为了解决通信过程中存在的大量行列格式转换问题,研究人员采用之前工作中提出的优化格式转换方法,该方法的核心策略是减小缓冲区的大小,提高缓存的命中率以及大粒度的数据移动。
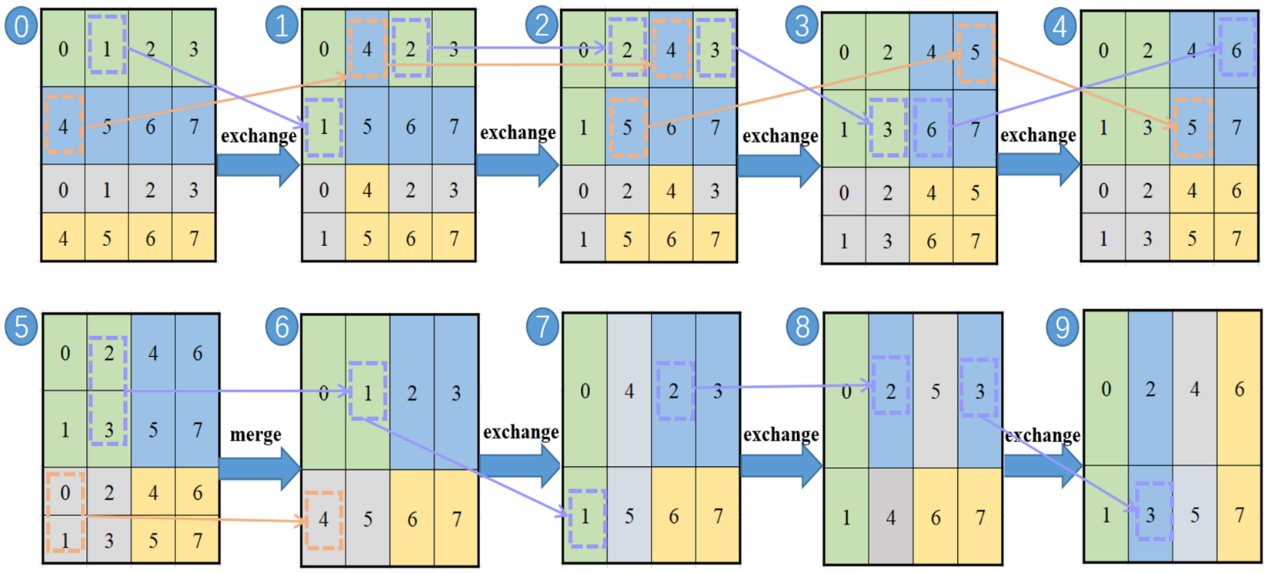
图5:优化的行列格式转换过程。
为了解决标准GW算法中计算介电矩阵时的存储瓶颈,研究人员设计了一种异步广播分块矩阵乘法,该方法只需要较小的缓冲区同时可以使用异步广播算法来隐藏通信时间。
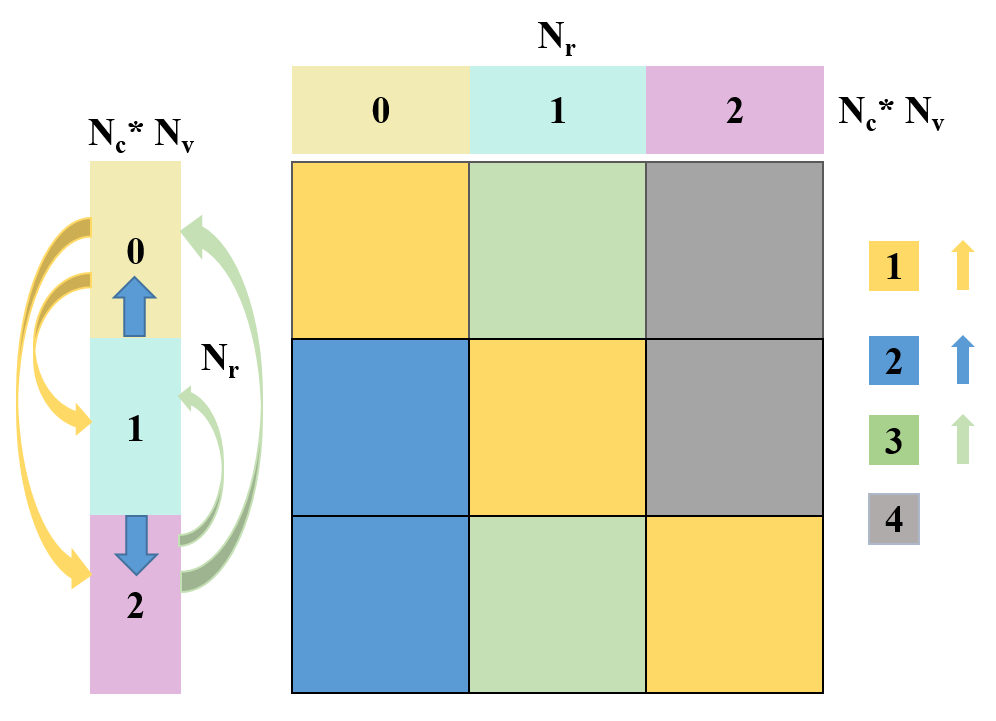
图6:计算CHI-0时的数据布局和分布式计算。
数值精度
PWDFT中的DFT计算结果和ABINIT软件进行比较,GW计算结果和BerkeleyGW进行比较。标准算法中,其计算结果是一致的。而低秩算法引入的误差低于0.1eV,相对误差低于2%。
表2:算法的数值精度

串行标度与CPE加速
研究人员以硅体系为例测试了算法的串行复杂度。结果表明算法为三次标度算法,同时由于很多特定优化的存在,标准算法的复杂度低于BerkeleyGW。同时研究人员在Li2916H2916体系中,测试了CPE的加速情况。结果表明,相比于MPE,CPE可以加速超过72倍。
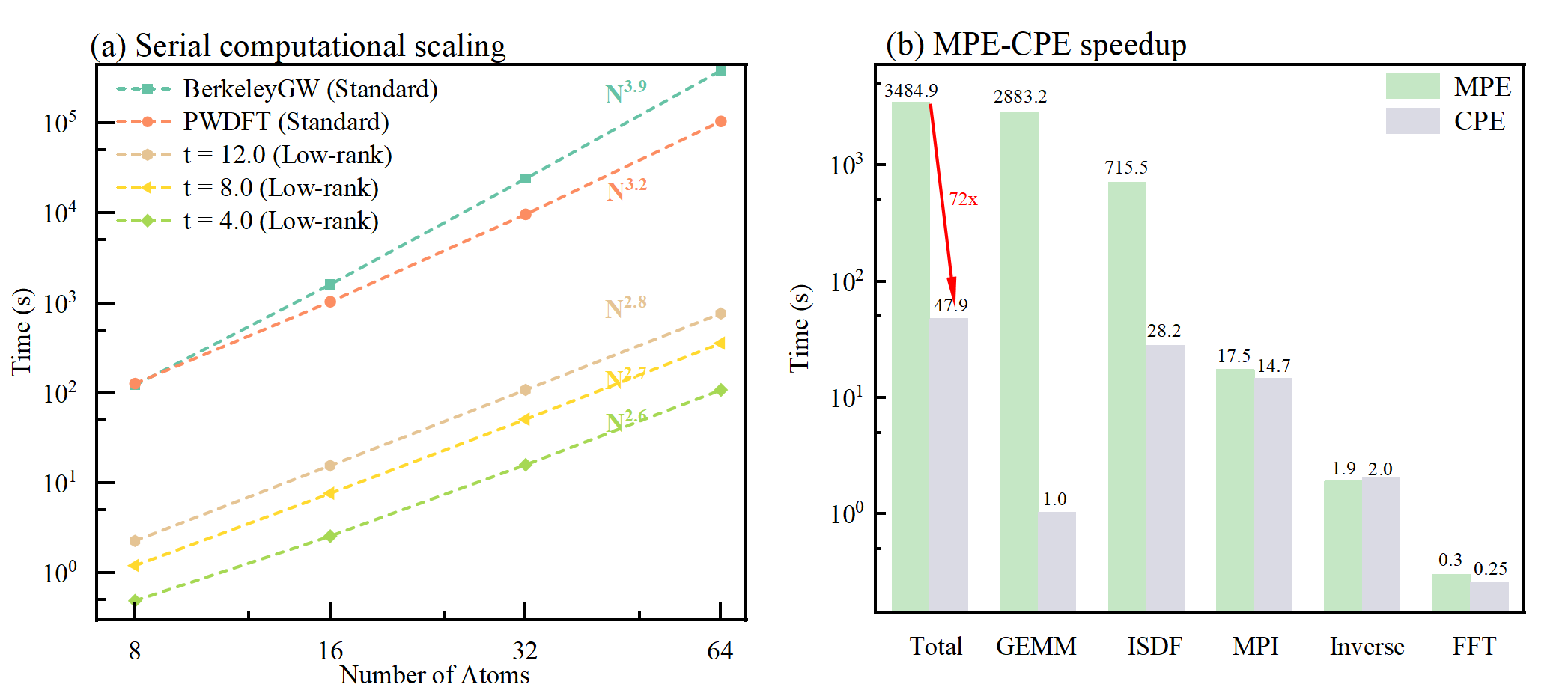
图7:串行复杂度测试及CPE加速。
强弱可扩展性
研究人员在LiH体系中对算法的强弱扩展性进行了测试。强扩展性测试在Li4000H4000体系中进行,结果表明,代码最大可扩展至260000个核心,并行效率为43.9%,表现出良好的强可扩展性。在弱扩展性测试中,通过将LiH单胞从8×8×8扩展至12×12×12,构建了多个测试体系。由于立方标度的算法在计算资源线性增长时,其理想扩展性为O(N²),而实际扩展性为O(N1.89),显示出良好的弱可扩展性。该算法最高可扩展至449280个核心,处理13824个原子。
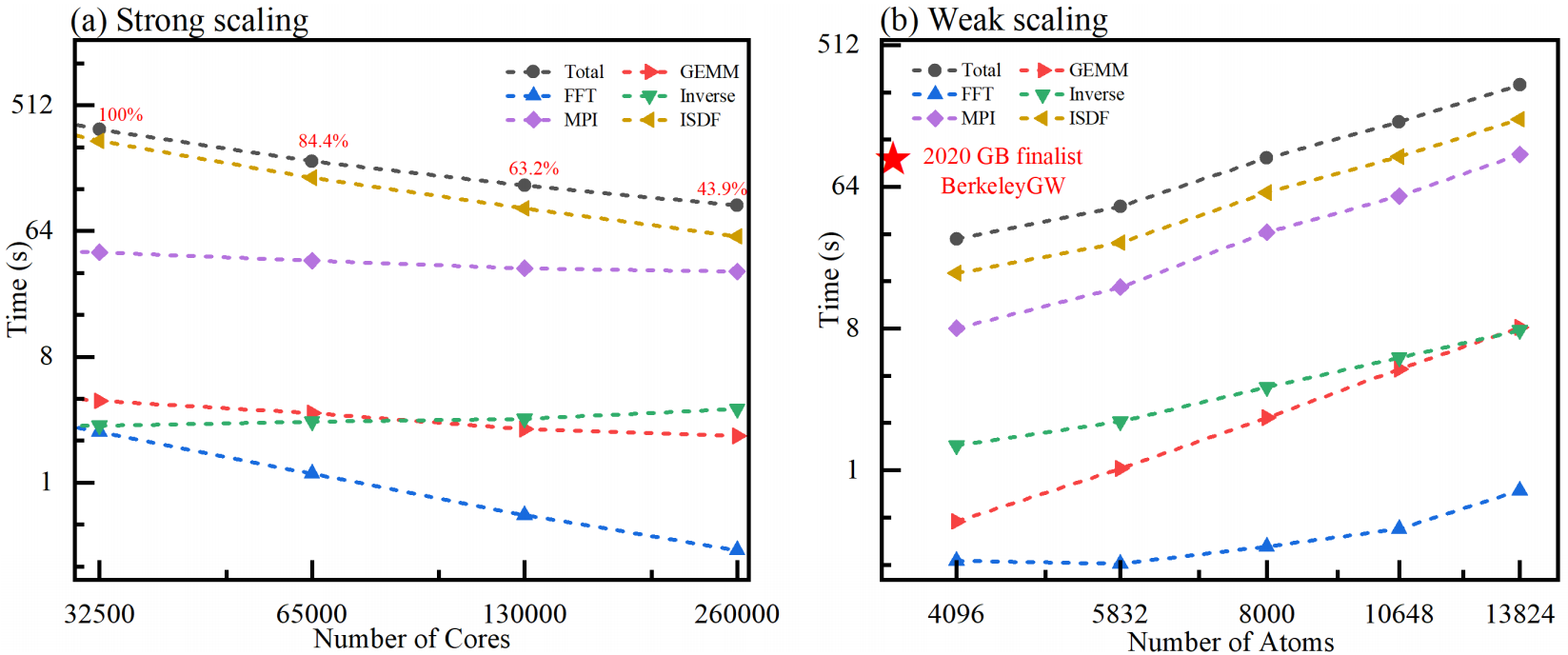
图8:强弱可扩展性。
论文题目:Enabling 13K-Atom Excited-State GW Calculations via Low-Rank Approximations and HPC on the New Sunway Supercomputer
作者:吴文挑,周正邦,姜庆彩,冯俊维,秦新明,马欢欢,曹振伟,陈俊仕,陈胜,孟鑫勇,侯昺焜,熊远帆,王林浩,孙艺轩,安虹,杨金龙,胡伟
通讯作者:胡伟
论文链接:https://dl.acm.org/doi/10.1109/SC41406.2024.00067
PWDFT软件介绍
PWDFT是一款基于平面波基组的密度泛函理论计算软件,主要通过求解Kohn-Sham方程实现固体材料和分子体系的电子结构计算和第一性原理分子动力学模拟。它与目前市场上的主流第一性原理软件属同类软件,并且具有相同的计算精度。
PWDFT使用C/C++语言编写,结合CPU-MPI和GPU-CUDA异构并行框架实现高性能计算,主要致力于实现数百到上千原子的大体系的密度泛函理论计算。目前支持单Gamma点和多k点采样,自旋限制、自旋极化和非线性自旋加自旋轨道耦合(SOC)的密度泛函理论计算,可以提供计算体系基态的总能量、能级、电子密度、态密度、磁性、原子力、能带结构,还支持结构优化以及激发态的电子结构计算、并有第一性原理分子动力学计算模块。
相比较其它国外第一性原理计算软件,PWDFT架构清晰,支持intel/Vtune 热点分析工具,在提高性能以及开发新功能、新算法方面具有独特优势。集成了最新的第一性原理加速算法,包括LOBPCG/PPCG本征值迭代算法、ACE、ISDF和PC-DIIS等加速算法,使得用PWDFT-DCU做大体系杂化密度泛函计算加速快100倍。支持CPU-DCU异构加速和CPU-GPU异构加速,现在可以同时兼容NVIDIA-CUDA和AMD-HIP平台。PWDFT的GPU优化程度比目前世界排名第一的第一性原理软件的GPU版本更高,并比其快了一个数量级以上。且具有非常好的扩展性能,这在平面波基组的第一性原理软件中名列前茅。行业内使用最广泛的第一性原理软件只能做到数百原子数百核并行,而PWDFT可以做到10000原子40000 CPU核并行,以及GPU/DCU上千块卡并行。

